Hanging in the Balance: Precision Weighing in Antiquity

Have you ever asked yourself, “Just how accurate was ancient weighing? Probably not, but that is what I ask myself almost every day as I struggle to understand Mesopotamian weights from the Bronze Age (3000–1200 BC).

I am not the first one to have asked the question. In fact, many scholars have contributed significantly to the study of ancient weights and weighing. One of the most comprehensive studies was conducted by Sir Flinders Petrie in 1926. Still cited today, Petrie collected information on some 4,000 weights from many sites across ancient Egypt as he attempted to identify specific weight forms and standard units through time.

Just as Petrie did for Egypt, but with electronic equipment and the benefit of 80 years of smaller studies since, I am gathering a comparative sample for greater Mesopotamia (modern Iraq, Syria, and parts of Turkey, Lebanon, Jordan, and Israel). Beyond gaining a better understanding of weights, my research focuses on the economic interactions and technological capabilities indicated by the act of weighing itself.

The most common weights used in the Bronze Age eastern Mediterranean were elongated stones reminiscent of dates or olives. Typically made of hematite, some were so highly polished as to result in a silver sheen. Other weights were finely carved in a variety of animal shapes, including bulls, lions, ducks, and frogs.These artifacts are easily recognized and often studied for their artistic interest. But most weights were not so intricate, and many were nothing more than roughly shaped stones. Difficult to identify and rather plain, these less-refined versions can get pushed aside in many investigations,evoking no deep fascination—at least not at first. However, if we ponder their larger implications they become some of the most intriguing finds.

One cloudy day in late November 2002, I was sifting through the artifacts stored in the Museum’s basement. I had examined countless weights and ejected many possible forms when I stumbled on a bag labeled “unfinished beads” from the 1922–34 excavations of Ur in Iraq. In their long storage, these ‘beads’ had been moved often and had lost their original field numbers. This made it impossible to relate them to a particular ancient building or level. Although this lack of information was unfortunate, I knew the artifacts could still tell me something.

There were 14 small stones in the bag, the largest only about 2 cm in length and the smallest less than half a centimeter. They were made mostly of banded agate in bright reds, whites, oranges, and browns. Their form was rough, but tapered, rather like a tiny olive or its pit. Many ancient beads had indeed been made in this form, but none of the 14 had been drilled through for a string. The excavators may have assumed they were a collection of beads that had not been finished by the ancient jeweler.

Agate was commonly used for beads, but it was also used in some cases for weights, and all of these small stones exhibited at least some flattening on one side—a feature typical of weights that allows them to sit in a balance pan without rolling. Moreover, these ‘beads’ followed an obvious progression in size. I immediately became more intrigued and placed each stone on my finest scales, recording its weight to a hundredth of a gram. Analyzing the numbers, however, I found no apparent logical sequence that compared to the known Mesopotamian unit of weight measure, the shekel.

Marvin Powell’s extensive research had definitively shown that the primary Mesopotamian shekel measured around 8.4 grams. My own data from the region (particularly from southern Mesopotamia) confirmed his results. Yet, the sequence I found based on the 8.4 gram shekel was confusing: 2/5, 1/4,3/20, 1/10, 1/20, and 1/60.

Was there a logical sequence I was missing? I knew that the Mesopotamian mathematical system was based on the number 60, so the unit of 1/60 of a shekel seemed to make sense.Perhaps converting to a common denominator of 60 would reveal something: 24/60,15/60,9/60,6/60,3/60, and 1/60.

And there it was. The progression was additive from three and above: 3 plus 6 is 9, 6 plus 9 is 15, and 9 plus 15 is 24. This progression is known as a modified Fibonacci sequence. At the unit of 1/20 of a shekel, it was a true Fibonacci sequence of 1, 1, 2, 3, 5, 8, where each successive number equals the sum of the preceding two numbers.

An additive sequence makes perfect sense for weighing with hand balances. Increasing the load by the next higher weight reaches the next in the sequence, and so forth. With several weights of each denomination, any amount could be assessed quickly and easily. And with the exception of the highest and lowest denominations in this set, there were multiple examples. The likelihood of this collection of shaped stones being a unified set of weights was now quite high. Not only were the objects similar in appearance, material, and manufacture, they also followed a logical, mathematical sequence based on their individual weights. But, what did it all mean for the process of weighing?

Most obviously, this set shows that the ancient Mesopotamians could and did weigh to very small units. It may not have been standard procedure for every transaction, but it was possible to weigh in small fractions of shekels. The capability of most ancient scales does not appear to have reached the level of 1/60 of a shekel (0.14 gram), but some must have been able to register this miniscule difference. Secondly, the set gives us a better picture of the process of weighing in tiny amounts. The person measuring would likely place weights in sequence until the scale became imbalanced, then remove the largest and place a duplicate of the second highest on the scale. If the pan was still heavy, the weigher would remove the duplicate and place the third highest, and so forth until the scales balanced. This would have been a painstaking process, probably involving a light, sensitive scale and some form of tweezers to move the tiny weights. Thus we come to the final, and broader economic implication of the set—there must have been something worth weighing in the tiniest of amounts. Perhaps this commodity was gold dust, rare spices, or some other light and costly material. Whatever it was, it was clearly of high value.

The smallest weight at 0.14 grams, or 1/60 of a shekel,seems out of place in the set, however. Perhaps it represents part of another sequence that was once present—also Fibonacci but at the unit of 1/60—and we are now missing the other pieces. If the smallest weight at 1/20 was too heavy, the weigher would then be able to move down to the 1/60 set and begin the process anew.

Regardless, the inclusion of the 1/60 weight is perhaps the most stunning of all the discoveries surrounding these artifacts. It is, in fact, the smallest physical example of an ancient weight ever recorded. Until now, the smallest reported ancient weight was a tiny hematite duck from Ishchali, near Babylon, that weighed 0.29 grams, or just slightly over 2/60 of a shekel. Interestingly , the existence of this 2/60 shekel weight in ancient Mesopotamia supports the hypothesis that a Fibonacci set based on the 1/60 unit was also used.

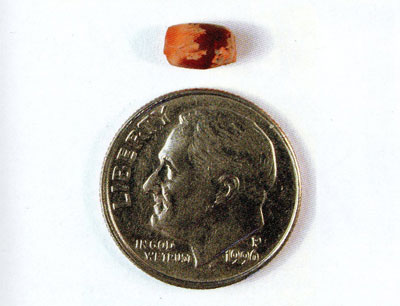
Could there have been an even smaller set? Based on the logic to this point, a smaller set would be at the level of 1/180 of a shekel (1/60 is 1/3 of 1/20, 1/180 is 1/3 of 1/60). This seems absurdly small, particularly for archaic balance scales, but the unit was certainly conceptualized. In their own cuneiform texts, Mesopotamian mathematicians often calculated miniscule sums, and they themselves defined their weighing system as based on grains of barley. The shekel, they report, consisted of 180 grains (sein Sumerian). Therefore, if the Mesopotamians physically measured at this level, they may actually have used individual grains of barley!

The smallest unit calculated in the cuneiform texts is the incredibly tiny 1/3 of a barleycorn. Such a weight would be approximately 0.0155 grams, or 1/540 of a shekel. Even if the ancient Mesopotamians measured to this level, which seems highly unlikely, our chances of finding the weights would be even smaller than the mass itself. Nevertheless, it is abundantly clear that the Mesopotamian understanding of fractions, mathematics, and weighing was extraordinarily sophisticated and that these ancient people placed a tremendous amount of ingenuity into miniscule levels of a weighty subject.