Roman Aqueducts

The aqueducts of ancient Roman times represent the efforts of government to provide city dwellers with an abundant supply of one of life’s necessities—water. Lacking any real understanding of the science of hydraulics, Roman en­gineers and builders were nevertheless able to construct long water channels of sufficient size and sturdiness to supply a city such as Rome with a quantity of water which was never again equaled until the nineteenth century. As simple as were the surveying instruments of the Romans, they proved more than adequate when used with care and were not substantially improved upon until the sixteenth century inventions of the plane-table, slit-and-wire sights, a separate sight rule of the form used today, and the true theodolite. During the seventeenth century the telescopic level appeared as a further aid in surveying.

In 312 B.C. Appius Claudius built the first aqueduct for the city of Rome. The Romans were still a tightly knit body of citizens whose lives centered on the seven hills within the city wall beside the Tiber river. This was as yet their only true Roman town, with the exception of their two small colonies established at Antium and Ostia. The population in Rome was increas­ing and, among other problems, the demand for drinking water placed a strain upon the old springs, wells, and cisterns of the community. Therefore, perhaps inspired by earlier Greek examples, Appius Claudius as Censor for 312 B.C. drew up and let out on contract the first proposal to bring water into the city from springs out in the countryside. The construction would be called an aquae ductus, a leading of water.

The Greeks had already created stretches of underground channels for bringing water to public fountains and reservoirs. Athens had at least one example and the island of Samos boasted a sixth century B.C. water tunnel excavated for more than 1000 meters through a mountain. The qanaat, an underground channel with vertical shafts at intervals along its length, was well known throughout the Near East in this same century. These ‘precedents were especially pertinent since Appius Claudius had no intention of creating a water channel above ground. The Celtic sack of Rome in 390 B.C. was still a topic for discussion and no one would deny that an exposed water channel in the countryside could be easily de­stroyed by an enemy army. Therefore the aque­duct was to be built entirely underground, some­what comparable in fact to the Cloaca Maxima, Rome’s already famous sewer. This latter was actually a roofed and channeled stream. Like it, the Aqua Appia was to run below ground in the city as well as in the open country. As in the case of the Samian .aqueduct and the Cloaca Maxima, the Aqua Appia would be an under­ground tunnel with a water channel running down the center of the floor, thus leaving a walkway on either side.

The method of surveying the Aqua Appia can only be surmised. No documents contemp­orary with its construction exist today to inform us. Frontinus, writing about A.D. 100, suggested that in earlier days the techniques of leveling had not been perfected. Sighting the line for the aque­duct along the ground from its source to the de­livery point in Rome could be easily if roughly accomplished by means of the groma, an instru­ment already in use among the Greeks. But the downward slope or gradient of the channel was also of importance. If the slope were constant and too greatly inclined downward, the running water could build up such pressure toward the end of its run that it would burst pipes and re­straining walls. Since the Greeks already had practical experience with this matter, it is not unlikely that the Romans acquired this knowledge from them in 312 B.C. More than a century earlier Rome had gone to Greece for advice in formulating its first law code. Now the aqueduct planners were using the Greek groma and they may very well have sought advice from Greeks on this matter of determining an adequate gradi­ent. Yet even without this assistance, the Romans could assume that conducting water from springs downward to Rome meant basically following land contours and grading the channel floor much like the bed of a river. Certainly they were fa­miliar with the causes and effects of swift cur­rents, eddies, and waterfalls in the Tiber or any stream.

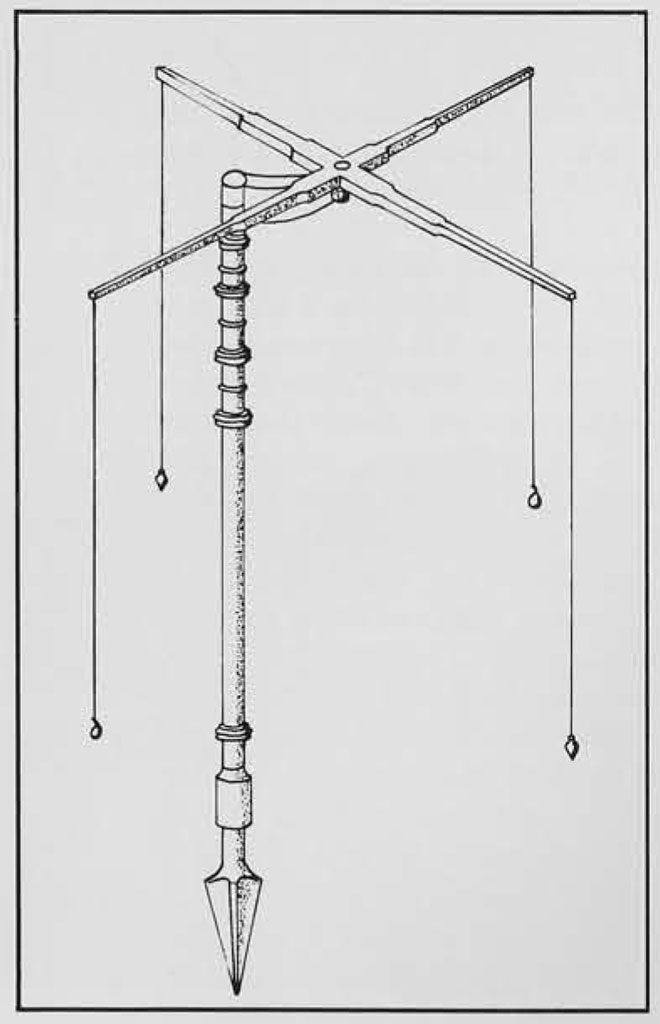
In the shop of Verus at Pompeii modern archaeologists discovered well-preserved bronze and iron fragments of a groma. Matching these with the description of the “star” or groma given by Hero of Alexandria, it is possible to achieve a rather accurate reconstruction. Four arms of equal length were joined at right angles at their inner ends to form a four-pointed star. At the central juncture, a pivot socket was set so that the star could then be placed to revolve horizontally on a pivot point rising at the end of an arm pro­jecting horizontally from the top of a vertical post. From each of the star’s points hung a line with a plumb bob attached. The instrument was em­ployed for sighting a straight line and, where desired, for sighting a cross line at right angles to the principal line. No calibrations are evident on the Pompeiian example nor did Hero mention any. The groma was thus a simple instrument employed for sighting straight horizontal lines. When used in conjunction with surveyor’s staffs (leveling rods) and measuring chains or cords, the groma proved adequate for Greek and Roman surveyors working on the geometric theory of right-angle triangles. Vertical heights and hori­zontal deviations could be calculated with suf­ficient accuracy for their purposes.

The plumb lines attached to the chorobates of Vitruvius, to be described later, hung across scales which indicated the horizontality of the instrument. Vitruvius did not invent this but was describing something already in use. The plumb lines were probably adapted from the con­cept of the carpenter’s level, an angular wooden frame with a plumb line to determine a true level by means of a simple scale. On the groma, how­ever, the plumb lines themselves actually seem to have been used for sighting. Since they hung truly vertical, two of them in a straight line through the central pivot of the arms could be lined up and used for sighting toward a surveyor’s staff or leveling rod. Of course, these plumb lines were completely exposed and could be set swing­ing by any breeze. For this reason an attempt was made to stabilize them by enclosing the plumb lines in tubes. But this made the groma less accurate and the idea of the tubes was aban­doned. Later, the groma was probably largely replaced by the dioptra whose trained operators, however, continued to be called gromatici.

When the Aqua Appia was completed after more than a year and a half of work, it supplied Rome with an estimated 54,750 cubic meters of water a day, and ran a course of little less than ten and one-third miles to cover the straight dis­tance of about seven and one-half miles between the springs and its distribution point in Rome. It had a collecting basin at its beginning but no terminal reservoir. Nor was a settling basin created along its route to collect such debris as stones and sediment carried along by the current.

Within the city and most likely in the countryside as well, shafts with footholes in their sides gave access to the channel for repairs or the removal of debris. In places, such as near its beginning, the channel lay as much as fifty feet below ground. Some stretches were tunneled through virgin rock, others were cut into the rock or soil as trenches, then lined with cut stone. Every foot was roofed over. Where mortar was needed plain clay served the purpose. Cement and lime mortar were as yet unknown to the Romans. With an average gradient of about 1 in 1500 (hereafter written as 1/1500) the aqueduct entered Rome at such a low level that it never could service the hilltops of the city. This need was eventually met by other aqueducts.

Almost three hundred years later, when Vitruvius wrote his work on architecture about 27 B.C., the situation in regard to aqueduct con­struction had changed considerably. Five of them now supplied Rome, new surveying instruments had appeared, and the techniques of manufactur­ing cement and concrete had not only- been learned but had been vastly improved. Cement seems to have been known to the Romans late in the third century B.C., while the earliest Roman concrete dates to the early second century B.C. By Vitruvius’ time the use of lead for pipes had been developed, and he could not only specify limits for the gradient of an aqueduct channel but also provide requisite thicknesses for lead pipe of differing sizes, and even describe the con­struction of siphons to carry aqueduct channels down hill slopes, across valley floors, and up the opposite hillsides.

Rome was now master of an empire. Popu­lation densities increased not only in provincial capitals but in smaller provincial centers as well. Not only was more municipal money available to improve local water service, but civic-minded citizens of wealth occasionally sustained the cost of aqueducts. Emperors on their state visits abroad often encouraged and even paid for the construction of local aqueducts. Throughout north Africa, in Spain, the Gauls, the provinces of Asia Minor, one aqueduct after another was built. The technical ability, if not locally avail­able, could be found among the army engineers assigned to each legion encamped at strategic points throughout the Empire. The municipal authorities had only to arrange with legionary commanders, either directly or through the pro­vincial governor, for the services of a librator or surveyor. It was he who established the line of the channel, the gradients, and such other basic details as the location of piers for aqueduct bridges.

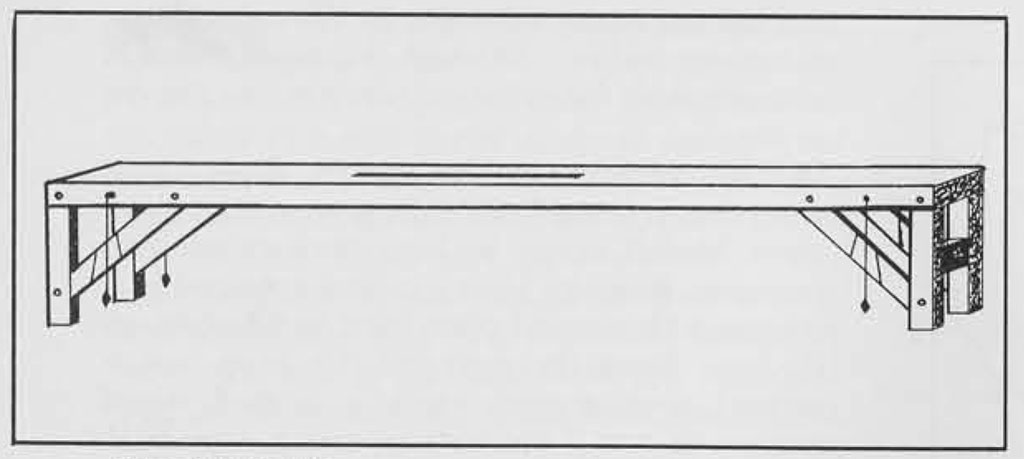
Vitruvius provided a choice of three instru­ments for laying out an aqueduct. There were the dioptra, the Libra aquaria (water level), and the chorobates. The dioptra and the water level tended to mislead, according to him, and he pre­ferred the chorobates. For this reason he de­scribed only the chorobates, ignored the groma completely, and gave no details on the dioptra or the water level. The chorobates as detailed by Vitruvius was both a water level and a series of plumb lines combined. The plumb line and bob formed part of a basic instrument used by carpenters and builders. Simple in form, it con­sisted of an angle formed by two pieces of wood fastened together. A crosspiece secured to each of these arms at the same distance from the center of the angle bore graded markings, the central one indicating a true vertical line for a weighted cord suspended from the center of the angle formed by the two arms. This Roman carpenter’s level appears to be related to the Greek compass or diabetes which may be one of the inventions ascribed to Theodoros of Samos who lived toward the end of the sixth century B.C. In fact the Egyptians did have a similar level at least by the 19th Dynasty (1349- 1197 B.C.). The fact that the shape of the Roman carpenter’s level is much like that of the Greek diabetes may perhaps explain the trans­feral of the Greek name to the Roman instru­ment.

The chorobates, whose description by Vi­truvius is rather clear, was a wooden plank twenty feet in length supported on legs at each end. The legs were fastened to the ends of the plank and also braced to it by short lengths of wood tenoned diagonally across the angle from each leg to the side of the plank. Plumb bobs were suspended from established points on the sides of the horizontal plank, at each end. By lining up the plumb lines against the proper calibration marks on the angular braces it was possible to establish the plank on a perfectly horizontal level. Since the instrument was used in the open air, however, practical experience demonstrated the confusion caused by any breeze which might sway the plumb bobs. Therefore an additional means of adjustment was incorporated in the piece. Turning to the concept of a water level, in the top surface of the plank the carpenter who manufactured the instrument cut a channel five feet long, one and a half inches deep, and one inch wide. When the wind made the plumb lines swing too much the plank was adjusted until water poured into this channel filled the channel evenly throughout its length. This meant that the surface of the water was at every point level with the surface of the plank. Therefore the plank itself was level. As an extension of this it would be possible to es­tablish a given angle of slope by marking the desired inclination on the inside of the water channel or, in the case of the plumb lines, on the angle braces. The plumb lines or the water surface would then be brought to this angle by tilting the plank from one end. This explana­tion makes it evident that the chorobates was never used for sighting. Vitruvius mentions it only in reference to leveling; he does not men­tion any slits or other apparatus attached to it for sighting. Therefore it was this instrument which he considered most appropriate for deter­mining the gradient in the channel of the aque­duct.

In its most direct application, the choro­bates would be set up on the channel floor being cut by the workmen. Keeping in mind the method of use and the cumbersome length of the chorobates, it is worth noting that by far the greater portion of any aqueduct was created in the form of an open trench to be roofed over. This facilitated the placement of the chorobates on the channel floor. The instrument was handled with similar ease on those portions of the channel raised on solid walls or arches. Where tunneling was employed, the chorobates could never have been lowered through one of the customary vertical shafts and shifted into a horizontal position on the tunnel floor. Certainly it would have been moved in from the end of the tunnel. The shafts were cut initially to faci­litate removal of rock during the tunneling pro­cess and also to provide the workmen with air. When the aqueduct was completed these could then he used by repairmen. In size, the shafts vary from about 30 inches square to about four feet square.

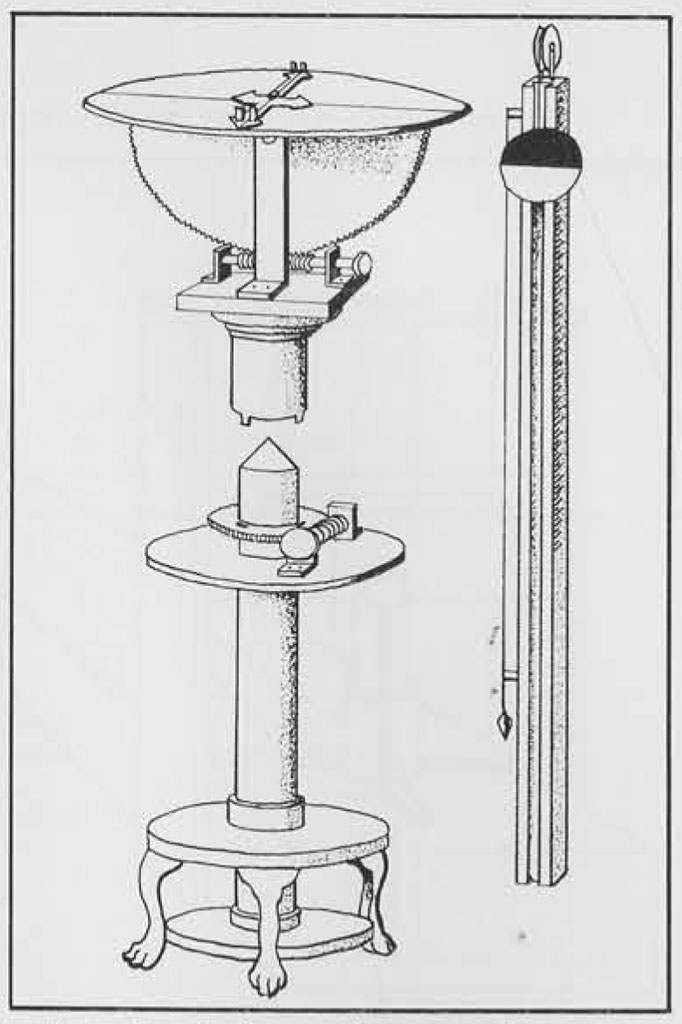
For the initial surveying of the aqueduct course and the establishment of reference points from which the chorobates could be operated, the librator must have used either the dioptra or the water level, the only other surveying instru­ments mentioned by Vitruvius. Writing about A.D. 65, Hero of Alexandria described a dioptra in detail but it seems hardly likely that this was the same instrument known to Vitruvius almost a century earlier. Although Vitruvius found it undependable for precision readings, the dioptra as detailed by Hero was indeed a precision in­strument entirely made of bronze. Since Vitru­vius’ time it must have undergone changes and Hero himself seems to have been responsible for some. Basically Hero’s dioptra consisted of a column with a round plate fixed horizontally on the top. From the center of this plate rose a vertical pivot around which a toothed wheel was set so that it could revolve in a horizontal plane. The teeth at one point in its circum­ference were engaged by a horizontal endless screw held to the bottom plate by two brackets. A groove equal in width to the thickness of the toothed horizontal wheel ran the length of the screw, thus leaving a segment devoid of sections of the screw threads. When this groove was turned to coincide with the edge of the toothed wheel, the wheel itself was left free to be re­volved rapidly by hand. The screw could be turned to engage the teeth of the wheel and lock it in position. Or the screw may also have been employed to make very precise turnings of the wheel. The elements described thus far formed the basic part of the dioptra. For taking the necessary readings Hero offered a choice of two attachments, each in the form of a column, either one of which could be set on the pivot and held by three vertical prongs fitting into slots in the toothed wheel surrounding the pivot. One attachment included a water level, the other had a theodolite.

In the case of the theodolite, two upright braces fastened to the top of the column held a vertical plate cut to the form of half a circle with teeth around the curved edge. This half plate revolved around a pivot passing through its thickness near the top horizontal edge, the pivot being secured in the upper ends of the braces. Between the bottoms of the braces ran a horizontal screw engaging the teeth of the half plate. A full circular plate was fastened hori­zontally to the top straight edge of the half plate. This circular plate was marked with two dia­meter lines at right angles to each other, one corresponding to the line of the vertical half plate underneath. The alidade for sighting, in the form of a narrow metal strip pointed at both ends and possibly with a sighting groove cut down the center of its length, was set to revolve horizontally around a pivot centered on the up­per surface of the horizontal circular plate.

The alternate attachment, the water level, consisted of a Doric column to be set over the pivot of the lower section and locked in position by prongs fitting into the horizontal toothed wheel surrounding the pivot. Atop this column was secured a long horizontal bronze bar or rod with a channel cut in its upper surface from one end to the other. A hollow bronze tube, with each end curved vertically upward, lay in this channel. From each upturned end of this tube projected a short length of glass tubing. The knowledge that two connected bodies of water will rise to the same level was employed here in this water level. When water was poured into the vertical glass tube at one end it flowed down into the bronze tube, running along its length and rising in the glass tube at the op­posite end. By sighting along the top of the water in each glass tube the surveyor could es­tablish a true horizontal reading. To facilitate this sighting, each glass tube had a small verti­cal bronze plate, cut with a horizontal slit, held against it by a vertical frame in which the plate could slide up and down. Each of these bronze plates was adjusted by a screw attached in its lower side and passing downward through the horizontal rod which projected slightly beyond the upturned tube. In general it would appear that this water level could be revolved only in a horizontal plane and was good only for estab­lishing horizontal levels. But with the sliding plates and the possible existence of calibrations on the plate supports it could also have been used for defining vertical angles. At least it could be used for sighting any straight line, horizontal or not, through rods and on to a dis­tant point.

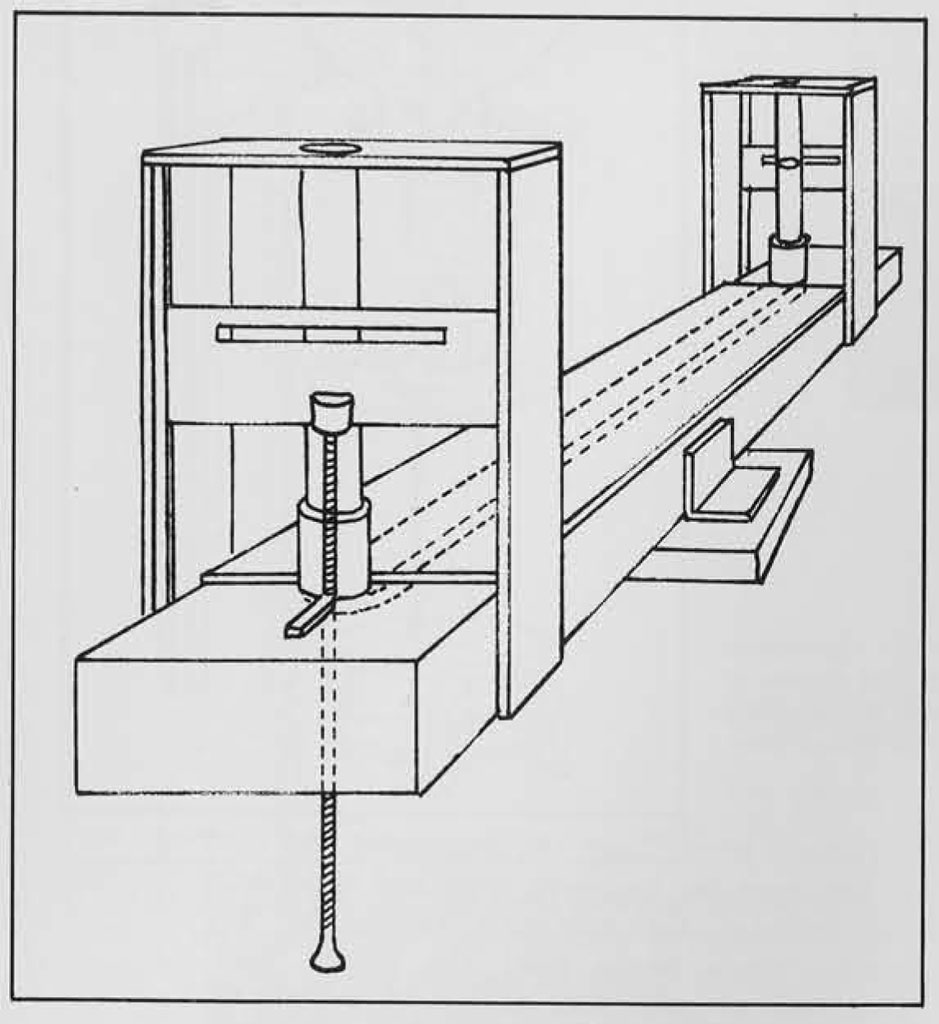
In regard to both dioptra attachments it must be remembered that in Roman times there was no such thing as a telescopic sight. But the leveling rod used with the dioptra was much like that employed by surveyors today. It had a vertical dove-tailed groove in its front face, in which was placed a sliding block with a flat disk or shield attached vertically to the front of it, the disk being painted black on one half and white on the other. The disk, with a sheet of lead fastened to its back to serve as a counter­weight, could be slid up or down by means of a cord tied to the sliding block and passing up­ward over a pulley on top of the leveling rod, then down the back of the rod to a point where it could be secured. To the back of the disk was also fastened a pointer which moved along a vertical scale marked on the side of the rod. On the opposite side of the leveling rod a hang­ing plumb bob indicated when the rod was being held perfectly vertical. The assistant holding such a leveling rod at a specified distance from the dioptra first made certain that it was in a vertical position on the ground. Then, on signals given by the librator, he adjusted the disk up or down until the dividing line between the black and white sections fell in direct line with the sights of the dioptra.

With these instruments and their trained operators at hand it was only necessary for the decuriones or local senators of the community to empower one of the town’s duumviri, the two men at the head of local government, to let out the necessary contract. In Rome this obligation at first fell on the Censor but then Augustus created the post of curator aquarum to control all aqueduct details. On receiving bids the duumvir would award the contract to a parti­cular business man or business combine. This contractor would then deposit with the govern­ment a certain sum of money as guarantee that the work would be satisfactorily completed. Any failure to live up to the contract could cause the forfeiture of this deposit. One con­tractor in Asia Minor did go bankrupt because of an improperly conceived plan for moving stone blocks in a construction repair project.

The first concern was to lay out the general course of the water channel from its source to the site where the main distribution reservoir would be located in the town. For this purpose a librator or surveyor was secured. From the sample problems given by Hero for the use of his dioptra it appears most likely that this initial survey for the aqueduct line was actually begun on the outskirts of the town and run up into the hills to the source of the water. On this first survey the librator was able to calculate the height of the source above the delivery point. He accomplished this by sighting horizontally along sets of leveling rods, marking them at the level of his sights and recording the heights of these marks above the ground level. This record was probably kept on sheets of papyrus. Mov­ing upward in this way over the rising ground, he accumulated a listing of vertical heights which, when totaled, would give him the height of the water source above the proposed terminal reservoir in the town. Using measuring chains or cords he could also record the horizontal dis­tance between leveling rods, and so find the total distance from the town to the water source. With these horizontal and vertical measurements he could determine the natural gradient of the line. Yet he also had the horizontal and verti­cal measurements for each section of the line. Deciding on an arbitrary length for each section, determined by the topography of the country­side, the librator then began to work his way back down the line from the water source.

Having decided upon the gradient for the first section. the librator set up his first leveling rod at the head of the line on the precise spot where it had been located when he finished sur­veying up from the town. Further downhill a second leveling rod was set up, again on a pre­cise spot marked during the first survey. Thus the two rods were accurately located along the line which would lead down to the town. Now he placed his dioptra between the rods so as to be in perfect alignment with them. Adjusting his sighting table to a perfect horizontal, he sighted back to the first rod where an assistant adjusted the black and white disk until its divid­ing line was set level with the dioptra sights. Then a staff was driven into the ground im­mediately next to the leveling rod and this was marked at the height of the disk’s center line. Without changing the dioptra, the surveyor next sighted down horizontally to the second leveling rod whose disk was also adjusted now to cor­respond to the height of the dioptra sights. A marking staff was set in the ground here and marked at the height of the disk. The dioptra then was moved downhill beyond the second leveling rod, adjusted to a horizontal level and sighted back to the second rod with the first leveling rod directly in line behind it. This meant that the dioptra was in the proper line toward the town’s proposed receiving reservoir and the first rod could be moved downhill be­yond the dioptra for further sighting. As he pro­ceeded with this second survey, the librator left in place the staffs marked with the reference heights from which vertical measurements would be taken down to the floor level of the proposed water channel. The entire concept of surveying for the gradient was based on the theory of right-angle triangles, conceived in a vertical plane with the lengths of both arms provided by the surveying measurements. By altering the horizontal distance from one rod to the next or by changing the vertical height of a staff marker from the ground it was possible to create a different gradient.

For measuring the distances necessary for these calculations Hero specifically indicated that measuring chains or cords were used. In the case of very short spans a measuring stick or regula could be employed. Hero also gave specifications for making a hodometer to meas­ure distances across the surface of the ground. This contrivance used toothed wheels geared in series to revolve one after the other. The wheels were of various proportionate sizes turning around axles in calculated ratios of revolution. The mechanism was enclosed in a box and at­tached to a carriage so that the initial toothed wheel could be turned by a single tooth on the inner side of the carriage wheel hub. The hodom­eter was always thought of as being placed in a vehicle. Since it measured only ground contours it can have been of little value for pro­viding true horizontal measurements needed by the librator. The emperor Commodus had a hodometer in his carriage as well as an ap­paratus indicating the passage of hours.

Moving his dioptra and rods on down the line until he finally reached the site of the pro­posed terminal reservoir, the librator could now see whether or not his final survey was correct. If all of his marked vertical and horizontal dis­tances provided totals equal to the master totals derived from his initial survey out from the pro­posed terminal reservoir, then everything was in order. Any discrepancy meant backtracking and correcting his established markers. It should be understood that librators demonstrated no inten­tion of maintaining a constant gradient for the entire length of an aqueduct channel. Such con­stancy is never found. A surveyor simply worked within understood limits. The gradients varied from one section to another and he understood that no section of the line could have a gradient so small that the water would move sluggishly, allowing sediment to settle and block the passage. On the other hand, an excessively large gradient over a considerable length of the course could permit dangerous pressures to build up, fractur­ing the channel or eroding its lining. Yet short lengths of very steep inclination were indeed created and suggest that the Roman engineer was less fearful of their limited use than he was of a slope that was too shallow. It may well be for this reason that Vitruvius and Pliny were con­cerned only with a minimum gradient.

Some confusion exists in the ancient Latin statements concerning the minimum gradient for an aqueduct channel. The manuscript of Vitru­vius indicates that the minimum must be one in two hundred (1/200). Pliny the Elder, writing nearly a century later, gave a figure of 1/4800. This discrepancy may well be due to some mis­understanding on the part of a medieval copyist working over Vitruvius’ text. Pliny’s figure is much more logical.

Existing remains of Roman aqueducts al­low measurements of their gradients and the de­tails prove rather enlightening when compared with the specifications of Vitruvius and Pliny. Rome’s Anio Vetus aqueduct of 272 B.C. has an average gradient of about 1/293, but over certain stretches it averages 1/250, 1/500, and even 1/1000. The Aqua Julia built for Rome in 33 B.C. shows 1/94 as its mean gradient while that of the Aqua Claudia, finished in A.D. 52, is 1/258. The latter at one point, however, drops 5.48 meters over a length of 10.90 meters as it runs down the side of a valley to cross a bridge over the Arno river. The city of Lyon in France had four aqueducts servicing it in Roman Imperial times. That known as the Aque­duct of Mont d’Or had a mean fall over its entire length of 3.59 meters per kilometer or about 1/279. Yet near its beginning it averaged about I / 143 through a length of five and a half kilo­meters. This led into a three and a half kilometer stretch with an average gradient of about 1/294. Nearer the city it reached about 1/476. The aqueduct known as La Brevenne has at one point underground a drop of 26 meters in a dis­tance of one kilometer. Later in its course it drops 90 meters over a length slightly less than three kilometers, for no apparent reason other than the slope of the land. These steep gradients occur in a course of the channel which ordinarily runs with a gradient varying from 1/667 -to 1/250. In other stretches the average gradient lowers to 1/1428 and approaching the city of Lyon it reaches 1/357.

The Lyon aqueduct of Craponne, though not well-surveyed for such details, descends in great steps and probably offers similar indications of great variations. It would appear that these first three aqueducts of Lyon were constructed between 29 B.C. and the death of Claudius in A.D. 54. But then there is a fourth aqueduct, that of the Gier, which apparently dates to the period of Hadrian (A.D. 117- 138 ) If indeed Hero improved the dioptra about the middle of the first century A.D. the more precise readings now possible might be evident in this aqueduct. Examination indicates that the Gier channel has an average fall of about 1/725, varying through the first two-thirds of its length from about 1/1177 to 1/625. After that, the channel aver­ages 1/800 to the distribution reservoir of Four­vieres in Lyon. Obviously the channel of this aqueduct runs more consistently at gradients lower than those of the other three aqueducts. While the improved dioptra may have played some role in the elimination of radical changes in level, the over-all gradient is related most directly to the long course of the Gier channel, amounting to 75 kilometers. The course of La Brevenne is about 55 kilometers in length while that of Mont d’Or is about 25 kilometers. The Gier river supplies water to the Gier aque­duct at 405.25 meters above sea level. The source of La Brevenne is 616 meters above sea level, that of Craponne about 700 meters above sea level and Mont d’Or starts at the fountains of Toux 350 meters above sea level. The Gier channel reaches its reservoir on the hill of Four­vieres at 292 meters above sea level; the others evidently arrive at lower levels. Of course, meas­urement of heights taken from sea level is a modern concept never known to the Romans.

The aqueduct of Nimes, with its famous Pont du Gard, has an average gradient of 1/2941 over its total length of 50 kilometers. Yet above the Pont du Gard it averages 1/1539, in the next stretch it runs about 1/5882, and toward the end it is measured at 1/2222. According to one estimate it supplied Nimes with at least 20,000 cubic meters of water in 24 hours. This aque­duct was completed by 19 B.C. The aqueduct of the city of Sens in France, with a total course of 4000 meters, has an average gradient of 1/2000 but over one stretch of 550 meters it drops 2.47 meters or 1/225. At another point its channel reverts to the other extreme with a drop of one centimeter in 820 meters or 1/82000. In view of the gradient variations evidenced in Ro­man aqueducts, it is interesting to note Pliny’s curious statement that if an aqueduct came over a great distance its channel should often bend up and down so as not to lose or affect the gradient.

The first Roman aqueducts were those con­structed for Rome itself and the earliest of these derived their waters from sources fairly close to the city. The Appian aqueduct (312 B.C.), the Anio Vetus (272 B.C.), and the Marcia (144 B.C.) were principally underground tunnels or covered trenches following land slopes and the sides of valleys. On the other hand, the Aqua Julia of 33 B.C. ran above ground for almost the last half of its length. Practically all Roman aque­ducts erected in the provinces date to the period subsequent to 27 B.C. when Augustus took firm control of the Imperial government. In this Im­perial period, surveyors more daringly carried channels straight through mountains and across valleys on series of arches or in some instances by siphons. Yet nearly every Roman aqueduct in France, Spain, Italy, and elsewhere has by far its major portion laid below ground level. In Tunisia the Zaghouan aqueduct, built under Ha­drian (A.D. 117-138) to service Carthage, col­lected water from springs and carried it 86 miles, of which little more than 12 miles ran on top of arches. Today, aqueduct arches too often give the impression that an aqueduct would look like this throughout its entire length.

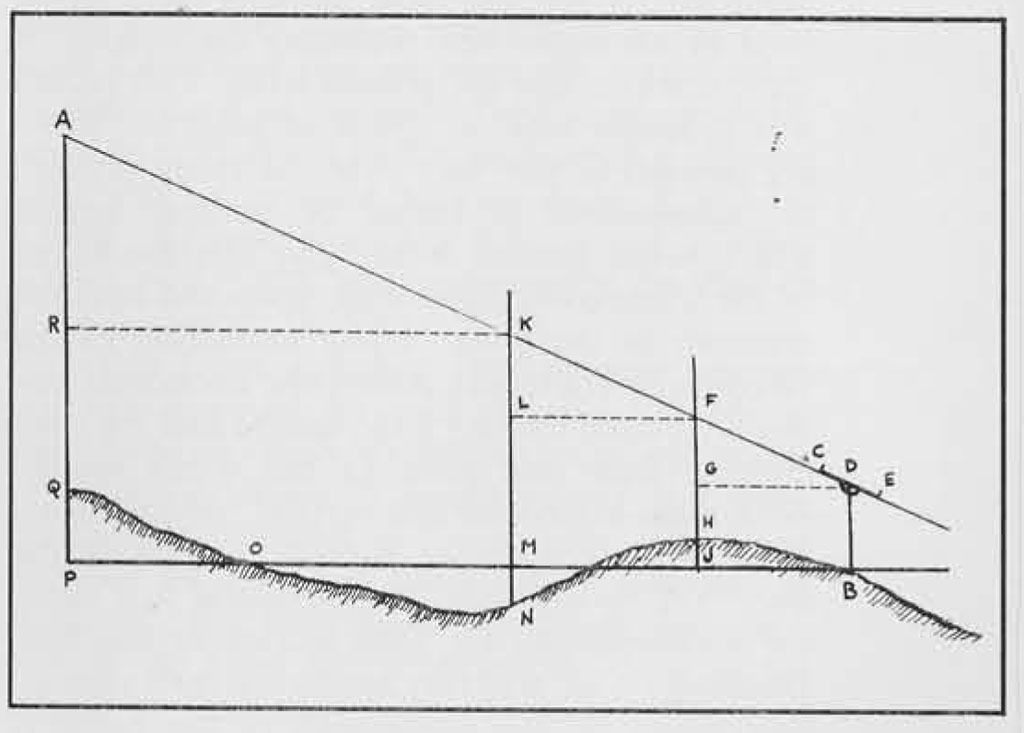
Charting the course of an aqueduct bridge across a valley was no difficulty for a Roman surveyor, and he marked a channel through a mountain using the same basic technique. Bring­ing the line of his proposed aqueduct right to the foot of the mountain and working continu­ously in the same vertical plane, he used his dioptra and several leveling rods to measure hori­zontal and vertical distances up the side of the mountain to the top in just the same way as he had done in making his initial survey. Again, the theory was that of vertical right-angle triangles. From the top of the mountain he then moved down the other side, following the same proce­dure until he had reached a point directly opposite his starting point on the first side of the moun­tain. Now he knew both the height of the moun­tain and the length of a horizontal line drawn through its base and corresponding to a horizon­tal line for the aqueduct channel. However, the channel would have to have a gradient. By ad­justing his paperwork to show this gradient, the librator then calculated how much farther down the far slope of the mountain he should set his marker to indicate the proposed tunnel opening. Now it would be possible for two teams of work­men to begin tunneling, one on each side of the mountain.

Once such surveying problems had been worked out and the proposed aqueduct line marked by posts, there was no further need for the professional librator. He was free to move’ on to other obligations. It was now time for actual construction work to begin and any additional surveying requirements would be of such a nature that they involved only verifying adherence to the details defined by the librator. Less highly trained personnel could handle this by referring to the librator’s records.

At this juncture the Contractors would have their Work crews already organized. Wherever possible these men were drawn from local com­munities along the route of the aqueduct. Even the smallest village could supply ordinary la­borers and in addition there would be a certain amount of slave labor involved—private slaves belonging to the contractors or slaves owned by government departments. Towns of moderate size could also offer a certain number of more specialized workers skilled in various aspects of heavier construction work. Supervisors, of course, would come from the headquarters of the contractor, who would be most interested in seeing that the project was successfully com­pleted.

Specialization among workmen had become rather highly developed by the first century A.D. and most workmen belonged to collegia, organi­zations somewhat like guilds. The operarii (or­dinary laborers) were just plain pick-and-shovel men; little but muscle power was demanded of them. On the aqueduct project, after they had finished their task of tunneling or excavating an open trench, then the ruderarii laid the rudus or crude rubble bedding of the channel. The cae­mentarii prepared the caementa (rough stones) and the lime and sand mixture as well as the finer mixture used for lining the channel. The

tectores (plasterers) applied this cement lining. Where stone blocks were needed for lining the channel in an earthen trench or for erecting an aqueduct bridge, these were trimmed to shape and size by quadratarii or lapidarii (stone cut­ters). The silicarii or parietarii laid these stones in lime mortar. In essence, all of these men, ex­cepting the operarii, were involved somewhat in masonry construction and so were classified as fabri structores. In this category also, ranked the arcuarii, men specializing in the building of vaults and arches. It was these latter workmen who set up any vaulted roofs required for the channel and who created the strong arches stretch­ing from pier to pier of an aqueduct bridge.

The librator represented another class of specialists who, operating with mechanical instru­ments and varying degrees of mechanical knowl­edge, were not required to perform real physical labor. Among these also were the machinatores (engineers operating cranes and other mechanical machines), the gromatici (technicians trained originally to use the groma but eventually cap­able of handling other surveying instruments), the mensores (surveyors particularly trained in measuring distances accurately), and the aqui­leges who may have been supervisors for seeing that all was properly done to accomplish the proper flow of water. Classified generally as artisans, the surveyors or libratores learned their skill ordinarily as apprentices to their fathers or to other surveyors. In some instances a librator may have had regular liberal arts schooling with subsequent studies under a geometrician.

Trenching the path for an aqueduct was fairly routine work using iron picks, shovels, Wicker baskets, and even leather buckets. The same tools, in addition to chisels and mallets, were utilized for tunneling which was indeed much like mining. To fracture rock the general practice seems to have been to build a fire on or against the rock surface, then throw vinegar on the heated rock. Cuniculus was the term used for a completed tunnel with its accompanying air shafts. Pliny specified that the shafts should be no more than 240 Roman feet (each 11.66 in­ches) apart but Vitruvius a century earlier had suggested a spacing of 120 Roman feet (one actus). Modern surveys of these ancient shafts show that the distances between them are fre­quently greater than either of these figures while at AIn-Djehal in Algeria they are 65 English feet apart. In tunneling through a mountain, it was probably the local gromatici and the men-sores who were responsible for maintaining the proper line and gradient already specified by the librator. That mistakes were made is shown by an inscription concerning the aqueduct at Saldae in Algeria (ancient Mauretania). Here the basic survey had been accomplished evidently in A.D. 148 by Nonius Datus, a librator from the Third Augustan Legion stationed at Lambaesis in the province of Numidia. Having completed his work, Datus handed over his plans to the gover­nor of Mauretania and returned to his legion. Before his departure, though, he had supervised the start of tunneling into both sides of a moun­tain along the aqueduct line. Later, working un­der their own local supervisors, the workmen ran into difficulties. In A.D. 152 the librator had to be recalled by the governor of Mauretania because the construction men, in tunneling from both sides of the mountain, had not been able to make the tunnels meet. Not only was the librator able to correct the problem, but also to demonstrate that the fault lay not with his master survey but rather with the local surveyors who had not adhered to his specifications.

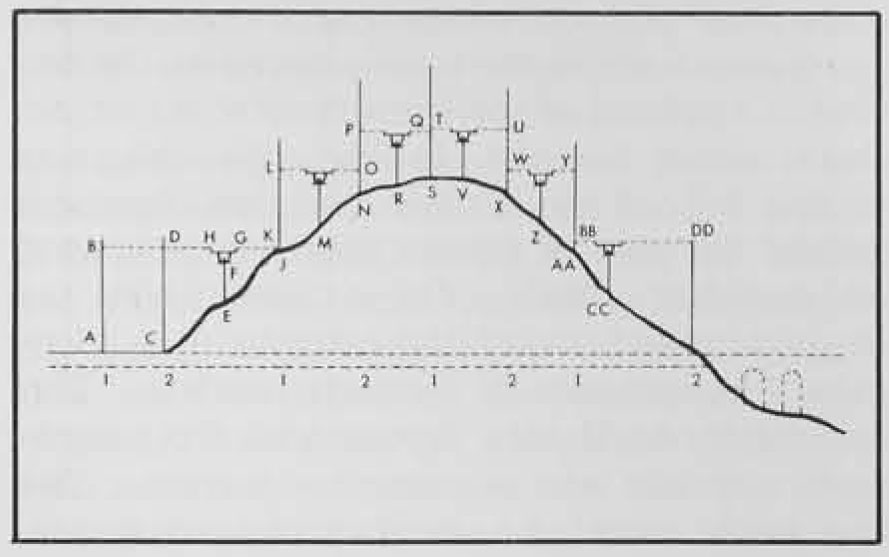
Constructing an aqueduct bridge involved first marking the locations of the piers and deter­mining their respective heights above ground level. This tatter figure was calculated again on the basis of vertical right-angle triangles. At the lowest point of the valley, the librator set up his dioptra in the true line of the proposed channel. On the approach slope of the valley, where the incoming line would make its bend to run hor­izontally across the aqueduct bridge, he placed one leveling rod with its disk set at the height of the channel. Then, further down the slope to­ward his dioptra, he placed two more leveling rods separated by a short measured interval. He now adjusted the dioptra’s sighting table verti­cally upward until he could sight through both of the intervening rods and up to the far rod high on the slope. On the intervening rods the sight­ing mark was set by the disks. The vertical height of the dioptra table above ground and the vertical heights of the disks above ground level were recorded. The horizontal distance from the diop­tra table to the first leveling rod and the horizontal distance from the first to the second rod were also recorded. By moving the dioptra and the leveling rods further up the slope in steps, the surveyor was able to create on his papyrus sheet a series of right-angle triangles with measured lengths and heights. A combination of these fig­ures provided him with locations for the piers and also with the particular pier height at any given spot where- his rods had been situated. Following this same procedure in the opposite direction he determined locations and heights for piers going up the far slope of the valley to the point where the channel would arrive.

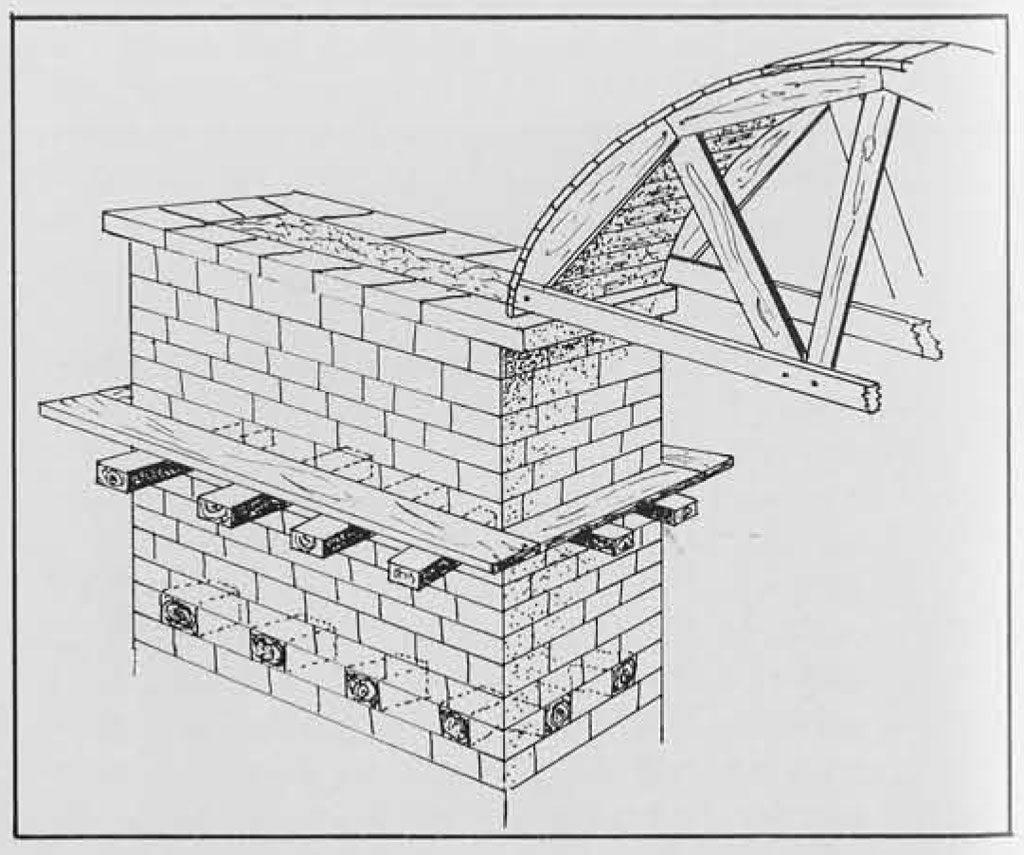
Now concrete and rubble foundations or simple stone foundations were laid for the piers, and on these the stonemasons or bricklayers be­gan erecting the four walls or faces of each pier. After a certain number of courses had been laid a mixture of rubble and cement was placed in the hollow center space. When the walls rose to a height at which the workmen found it difficult to proceed further from the ground level, beams were placed in or across the finished work so that they projected from the sides. Several further courses of stone or brick were laid over the beams to stabilize them and then, on these projections, boards were set to serve as platforms for the men who now were enabled to continue the walls up­ward. This creation of platforms, supported by beams set into the masonry, was repeated again and again as the piers rose higher. From these platforms, not only could the walls be built but the rubble filling of the core could also be handled. The stone rubble and the cement mix­ture of lime and sand were not in Roman practice prepared as one substance for pouring. Instead, the stones would be set in layers by hand, then covered with the cement mixture which ran down among the stones. All of these materials, even the building stones and bricks, would be hoisted up to the workmen by cranes with pulley arrange­ments, utilizing varieties of clamps and cradles.

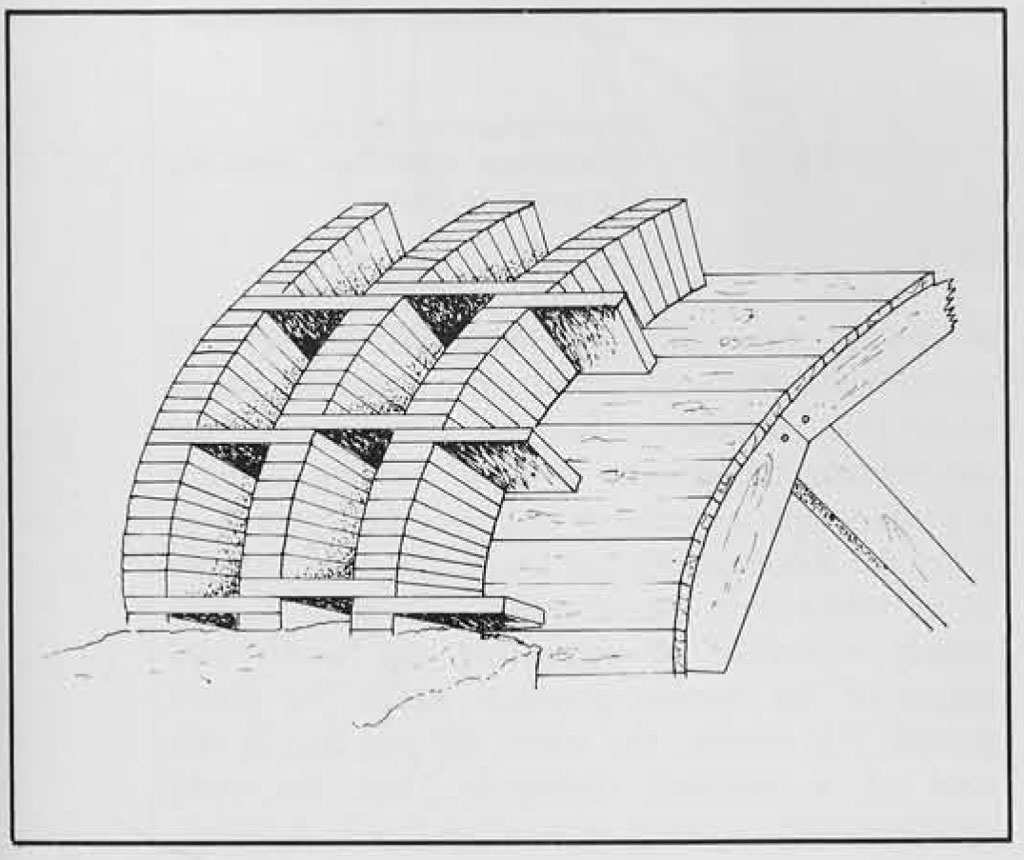
When the piers were completed to their pre­determined heights they could, if necessary, be checked for the proper level by stretching a plank from one pier to the next and placing a choro­bates on it. Since such a span ordinarily ran from 5 to 5.5 meters but might be as great as 6.2 meters, this means that the chorobates itself would in most cases be able to cover the distance. Next it would be time to construct the arches reaching from pier to pier. For this the car­penters formed wooden frameworks, the ends of which rested on projecting stones (corbels) or on the straight edges of the piers’ upper surfaces. This could mean that the springs of the arches would be set in from the sides of the piers. If the design did not call for such a setback, then the top of the pier might be finished with a pro­jecting cornice and the arched framework rested on this. Of course, for low aqueduct arches the scaffolding could rise directly from the ground. Stone or brick ribs were Iaid on the wooden frame, the horizontal sides above the piers were constructed, and cement and rubble were filled in behind. Then the longitudinal side walls of the entire bridge were built up to the proper height. The space between these longitudinal walls was filled in with cement and rubble to the level of the water channel floor. Again, the floor’s proper level or gradient could be checked with the chorobates. Then this floor surface and the vertical side walls of the channel were coated with cement. Last of all the channel was covered with a vaulted or fiat roof. Among other reasons, this covering was necessary to prevent accumu­lation of dirt and debris in the water. Vitruvius indicated that the entire water channel should be covered so that a minimum of sunlight would reach the water. He was aware that this would prevent evaporation, but to him and other Ro­mans evaporation meant not just loss of water but loss of the wholesome elements of the water. When all of the cement and concrete had set, then the wooden framing for the arches was removed. Similarly, the platforms around the piers were taken down and the supporting beams, imbedded in the masonry, were trimmed off. Removing them entirely would have damaged the masonry. In time the remnants of wood disintegrated, leav­ing cavities in the face of the wall. These could be filled in or left as they were.

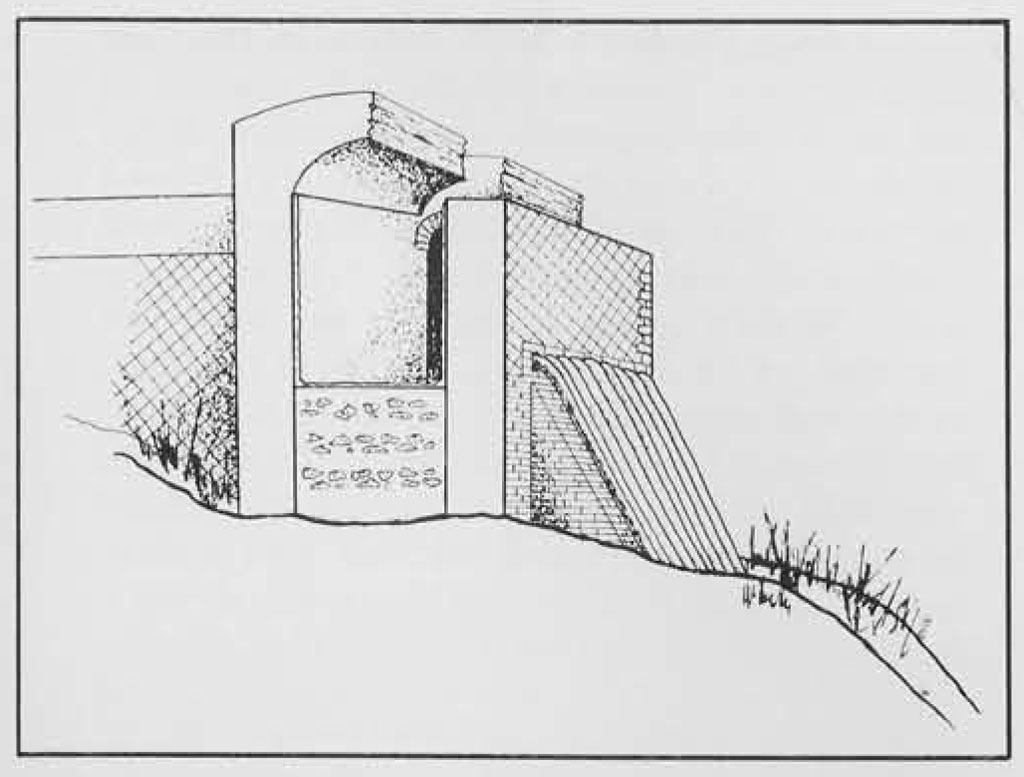
In some instances the Roman engineers chose to avoid designing extremely high or long aqueduct bridges and, instead, carried the water across intervening valleys by siphons. Today these are often termed reverse siphons, but in effect they were simply lead pipes run down one side, across the bottom, and up the other side of a valley. No true siphon effect was present, the concept being that of a U-tube. Water was run into a receiving reservoir and then diverted into a number of small, strong, lead pipes which car­ried it across the valley to a reservoir on the opposite side situated at a level lower than the first reservoir. As Pliny said, “Water rises as high as its source.” An ordinary stone or cement chan­nel could not have withstood the pressures built up as the water reached the bottom of the valley. This pressure is calculated in terms of atmos­pheres, one atmosphere equalling the pressure of air at sea level or 14.7 pounds per square inch. At first, the Romans did use on occasion blocks of stone locked together and having a circular channel cut through them. Then they turned to terra-cotta pipes bedded in stone or cement, and eventually they came to prefer the use of lead pipes protected with stone or cement at bends where the pressure would be greatest. As for determining the volume of water flowing through a given length of pipe in any specified period of time, the Romans did not know that velocity had to be taken into consideration. To them it was simply a matter of measuring the width and height of the section through which the water passed. Of course, the water did not rise to the roof of a channel ordinarily, but the only measurement recorded in modern times, in regard to the actual height of the water in the channel, comes from the Aqua Marcia at Rome. Near its source the channel measures 1.7 meters wide and 2.5 meters high, but the lime encrustations on the sides show that the water height was normally 60 centimeters. Using these figures it has been estimated that the Marcia supplied Rome with 140,700 cubic meters of water per day. In a lead siphon pipe the water would certainly fill the cross-section completely. Here the Romans were on a bit safer ground in esti­mating the delivery capacity of pipes of various sizes even though they did not evaluate velocity or pressure.

The Anio Vetus, completed in 270 B.C. for the city of Rome, may have included a siphon, and the Aqua Marcia of 140 B.C. had one run­ning from the Quirinal to the Capitoline Hill. Pergamum’s aqueduct of 180 B.C. had a siphon which may have sustained a pressure of 20 at­mospheres, and by 134 B.C. the Italian city of Aletrium boasted an aqueduct with a siphon. At Lyon the Mont d’Or aqueduct had two and possibly three siphons. The Gier aqueduct had four siphons.

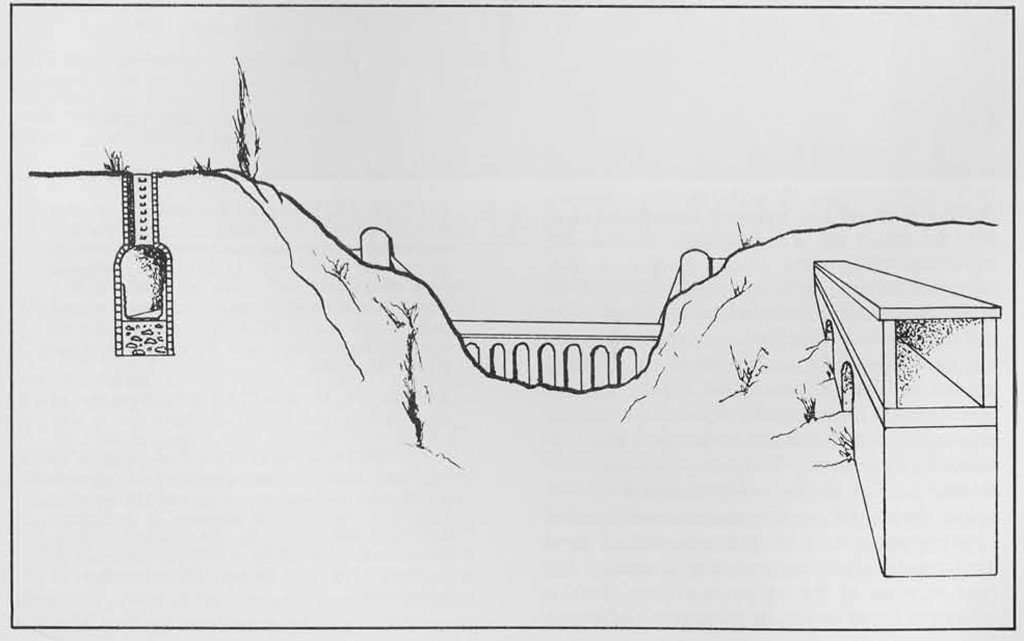
Taking the Saint-Genis siphon in the Gier aqueduct as a typical example, it is possible to see the Roman engineer’s comprehension of his problems. At one side of the valley, the channel from the Gier river flows into a cement-lined reservoir 21 feet long by 7 feet 4 inches wide, with a vaulted ceiling springing from walls five feet high. A bit more than a foot above the floor, in the wall opposite the entrance, are nine open holes, each 8.7 inches in diameter. From these, nine lead pipes, formed of lead sheets molded around wooden cores and soldered with a mix­ture of tin and lead, carried the water down a drop of 266.5 feet to an arched bridge 65 feet high and 24 feet 10 inches wide, leading 442 feet across the valley bottom. Rising up the opposite side, the pipes entered the receiving reservoir at a height about 19 feet below that of the initial reservoir. In all, the straight distance between the two reservoirs is about 2925 feet. At a later point in its course the same channel runs through another siphon of nine pipes and still later, an­other of eight pipes. The number of pipes in the fourth siphon cannot be determined. These ex­amples are sufficient, however, to suggest that the Romans distrusted the ability of their large lead pipes to withstand high water pressures generated in aqueduct siphons. They preferred to divide the water and carry it through the valley in a multiple arrangement of small, but stronger, lead pipes. Calculations based on the siphons of the Gier aqueduct suggest that this one channel could supply Lyon with about 24,000 cubic meters of water in 24 hours. The La Brevenne aqueduct may have supplied 28,000 cubic meters in 24 hours.

Siphons, gradients, cement, the groma, the chorobates, the dioptra, geometric principles—with the instruments, the construction techniques, and the practical and technical knowledge avail­able to them, the Romans built innumerable aqueducts which serve as one symbol of their advanced culture. By rough count more than 80 major Roman aqueducts can be identified today and others await idenification or thorough study for publication. In ancient times all of them needed constant attention and repair. As the years passed these repairs were more crudely accomplished and new aqueducts were less sub­stantially constructed. The Aqua Alexandrina of about A.D. 226, the last aqueduct built for Rome before the central government was transferred to Constantinople in A.D. 330, was still of good workmanship but less carefully finished. Yet even in some of the earlier aqueducts there is evidence of cost cutting at the expense of sturdy construction. As life in the western portion of the empire became more disrupted, less atten­tion was given to maintenance of the aqueducts and many succumbed to the forces of disinte­gration or the barbaric invaders. Yet even through the Middle Ages a few of the ancient aqueducts, roughly restored, were able to provide such cities as Paris with much-needed water. New aqueducts built for Rome in the Renais­sance, and even as late as the nineteenth century, either utilized the course of ancient chan­nels or tapped their same water sources. Through their interest in good water supplies, the Romans were able not only to satisfy the daily needs of citizens but also to provide communities with an abundance of public baths and ornamental foun­tains. Today the ancient Roman Empire is famous for its aqueducts and its roads. Both owed their existence to the skills of the same surveyors whose abilities were not equaled until modern times.